寫在前麵：

延遲開學的日子（zǐ），是自我調整的日子，是彎道超車的日子，是探索屬於自己的學習方式的日子。居家學習更需要同學們安排好學習時間，提高自主學習的效率，寧願一時受冷蹲在屋頂蹭網，不貪小小溫（wēn）暖躲在被窩打卡。居家學習的二輪複習階段要注（zhù）意以下幾個方麵。

作者：張培強，徐州一中高三（sān）年級數學教研組長

一、製定二輪（lún）微專（zhuān）題複習計劃。根據學校網課的安排，以及自身的學習情況，製定適切的二輪微專題複習計劃，將自己的弱項納入到計劃中，每天都要通過訓練與反思對弱項問題進一（yī）步強化提升，嚴（yán）格執行複習計劃，提高時間效（xiào）益。

二、提（tí）高上網課的效率。及時完成老師布置的任務，標記疑難，做好（hǎo）提問的準備。上網課的時候跟上老（lǎo）師或發言同學的思路（lù）進行思考，積極參與課堂的互動，及（jí）時（shí）有（yǒu）重（chóng）點的做好筆記（jì），整理解答過（guò）程。

三、堅（jiān）持每天的基（jī）礎訓練。操千（qiān）曲而（ér）後曉聲，觀千（qiān）劍而後識器。從現在到高考，都要堅持基礎題的熟手訓練。根據老師布置的基礎訓練，結合自（zì）己手裏的材料（liào），做到每天進行一次基礎訓練（liàn）。

四（sì）、繼續強化中檔題的訓練。每天安排一次中檔題訓練，包括填空題中的第10-13題，解答（dá）題中的第17-18題，理科（kē）再加上第22題，及時按高考評分要求批改、訂正、反思（sī），總結方法，積（jī）累經（jīng）驗，提升能力。

五、整理錯題做好反思。題海無邊（biān），反思才能幫你到（dào）岸。及時整理錯題，反（fǎn）思錯因，優化方法，積累經驗。對於自己的（de）高頻易錯點，可以將做過的類似題翻出來再做、再（zài）反思（sī），以達到（dào）解一題，通一（yī）類之效。

六、深化對題目的研究（jiū）。數學家哈爾莫斯說過：問題是（shì）數學（xué）的心髒。數學家波（bō）利亞說（shuō）過：掌握數學就是意（yì）味著善於解（jiě）題（tí）。學數學，歸根（gēn）結底在於對題目的研究。在常規的解題訓練（liàn）之外（wài），每天可以安（ān）排一道（dào）題目的深入解決，將你的探索曆程記錄（lù）在一個專門的本（běn）子上。

關於解題，在（zài）數學的江湖中流傳著“五重境（jìng）界”說：

第（dì）一層境界：正確（què）解題（tí）

兵來將擋，水來土（tǔ）掩，見招拆招。很多同學以為如果一道題（tí）目做錯，訂正一下，知道哪裏錯了，怎麽做，就行（háng）了，其實這隻是最低境界。

第二層境（jìng）界：一題多解

多點開花，條條大道通羅馬；似倚天劍（jiàn）輕靈無雙，劍（jiàn）招（zhāo）千變萬化，虛（xū）實相間，誰與爭鋒。91成人版要養成的良好習慣是，不要滿足於用一種做法和思路解題。一道題目做完之後想一想還有沒有其它方法，哪種方法（fǎ）更簡單。對於最（zuì）後（hòu）的結（jié）果，是不是可（kě）以有其它的合理解釋。

第（dì）三層境界：多題一解

以靜製動，以不變應萬變，一招（zhāo）製敵（dí）；似玄鐵神器，重劍無鋒，卻剛（gāng）猛異常（cháng），一劍揮下，縱它千百變（biàn），亦必摧之。完成（chéng）一道（dào）題目的分析後，嚐試推而廣之，或者把其中（zhōng）的數字換成字母，或者把一（yī）些條件做一些改變，從這道題目延（yán）伸出去，探究與此相關的一類題目。

第四層境界：發現定理

無招勝有招，漸成大家；至此境界，草木皆為利刃，隨心所欲，敵未動，已斃於無形。到了這（zhè）個境界（jiè），可（kě）以自己發（fā）現一些結（jié）論（lùn）或定理、規律。這些（xiē）結論、定（dìng）理規律都是解題（tí）的有用工具（jù）。解題高手都有自（zì）己的定理庫。

第五層境（jìng）界：自（zì）己編（biān）題

自成一派，獨孤求敗；高處不勝寒，自己跟（gēn）自己玩解（jiě）題的最高境界是（shì）能夠（gòu）編題。不是所有的人都（dōu）具（jù）備編（biān）題的能（néng）力。解（jiě）題高手拿到一道題（tí）目，會知道出題者的意圖，會（huì）發現出題者（zhě）的陷阱。即便出題者粗心出現了一個錯誤，他也能（néng）夠很快地糾正糾偏。

同學們，你（nǐ）可以先自我（wǒ）判斷一下，你現在（zài）在那一層呢（ne）？

下麵，以一道題（tí）目為例，與同（tóng）學們一塊經曆這五重境界：

例．已知正數x，y滿足x＋y＝3，則

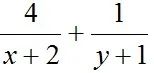的最小值為________．這樣一類多元最值問題，91成人版見過幾十遍了，是考查基本不等式的常見題型。

第一層境界（jiè）：正確解題相信多（duō）數同學都已（yǐ）經達到了，不必多言。

第二（èr）層境界：一題多解這一層，相信很多同學也都能娓娓道來。首（shǒu）先，可以采取消元的方式，得到一元的分式和（如

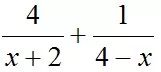），之後考慮導數求最值、通分後使用基本不等式等均可；其次，采用“1”的代換，將待求乘上

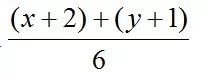（也就是1），展開後使用基本不等式即可。（關於這類問題的解決（jué），如果你（nǐ）還有疑問（wèn），可以掃碼（mǎ）回看市（shì）彭城課堂的（de）微課：基本不等式的（de）基（jī）本模型）

第三層境（jìng）界：多題一解（jiě）

到這一層，我（wǒ）們（men）要把（bǎ）題目（mù）進行歸類提煉。這類題目無非是已（yǐ）知兩個變元的和（hé）求倒數和的最小值，或已知兩個變元的倒數（shù）和求和的最小值，即下麵兩（liǎng）個題型：題型1：由△＋□＝6，求

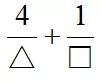的最小值；題型2：由

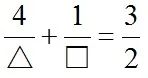，求△＋□的最小值。

第四層（céng）境界：發現定（dìng）理

過了第三層，你能熟（shú）練將題目題型化、套路化了，這可（kě）以助你解決（jué）高考中的大部分題目。接著，你要思考的是：還能再優化一下，再省勁一點嗎？91成人版不妨把“1”的代換過程（chéng）變一下形，得到

（常數），再嚐試一般化，就可以得到：

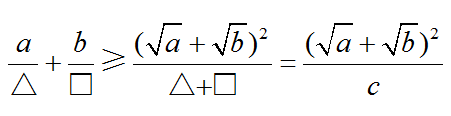（常數），最小值就直接出（chū）來了（這其實就是盛於數（shù）學江湖的權（quán）方和不等式）。

第五層境界：自己編題

解題，要經曆“見山是山，見山不是山，見山又是山”的參悟過程。就如同“1”的代換，1非1，實為形式非1而實質是1，1還是1。那麽“△”、“□”是什麽？是x，是x＋2，也是sin x，

如此，題目就（jiù）源（yuán）源不斷地來（lái）了。

同學們（men），你Get到了嗎？

數（shù）學家波利亞指出：“好問題（tí）同某種蘑菇，有些相像，它們成（chéng）堆地生長，找到一（yī）個以後，你就（jiù）應當（dāng）在周圍找一找，很可能附近就有好幾個。”問題解決隻是解題的第一步，之後（hòu），從（cóng）解決（jué）的問題出發，運用（yòng）類（lèi）比、聯想、特殊化、一般化等思維方法，創編派生出一些常規問題和開放性問題，使得問題“成（chéng）片開發”，提升素養。或許，在不久的高考（kǎo）考場中，你會見到你自己（jǐ）編的題。